ホーム » 最小共分散行列式

「最小共分散行列式」カテゴリーアーカイブ

PyOD 0.8 : Examples : 最小共分散行列式 (MCD)

06/27/2021

PyOD 0.8 : Examples : 最小共分散行列式 (MCD) (解説)
翻訳 : (株)クラスキャット セールスインフォメーション
作成日時 : 06/27/2021 (0.8.9)

* 本ページは、PyOD の以下のドキュメントとサンプルを参考にして作成しています：


* ご自由にリンクを張って頂いてかまいませんが、sales-info@classcat.com までご一報いただけると嬉しいです。

 

★ 無料 Web セミナー開催中 ★ クラスキャット主催 人工知能 & ビジネス Web セミナー

人工知能とビジネスをテーマに WEB セミナーを定期的に開催しています。
スケジュールは弊社 公式 Web サイト でご確認頂けます。
  • お住まいの地域に関係なく Web ブラウザからご参加頂けます。事前登録 が必要ですのでご注意ください。
  • ウェビナー運用には弊社製品「ClassCat® Webinar」を利用しています。
クラスキャットは人工知能・テレワークに関する各種サービスを提供しております :

人工知能研究開発支援 人工知能研修サービス テレワーク & オンライン授業を支援
PoC(概念実証)を失敗させないための支援 (本支援はセミナーに参加しアンケートに回答した方を対象としています。)

◆ お問合せ : 本件に関するお問い合わせ先は下記までお願いいたします。

株式会社クラスキャット セールス・マーケティング本部 セールス・インフォメーション
E-Mail：sales-info@classcat.com  ;  WebSite: https://www.classcat.com/  ;  Facebook

 

 

PyOD 0.8 : Examples : 最小共分散行列式 (MCD)

完全なサンプル : examples/mcd_example.py

 

合成データの生成と可視化

pyod.utils.data.generate_data() でサンプルデータを生成します :

from pyod.utils.data import generate_data

contamination = 0.1  # percentage of outliers
n_train = 200  # number of training points
n_test = 100  # number of testing points

X_train, y_train, X_test, y_test = generate_data(
    n_train=n_train, n_test=n_test,
    n_features=2,
    contamination=contamination,
    random_state=42
)

X_train, y_train の shape と値を確認します :

print(X_train.shape)
print(y_train.shape)

(200, 2)
(200,)

X_train[:10]

array([[6.43365854, 5.5091683 ],
       [5.04469788, 7.70806466],
       [5.92453568, 5.25921966],
       [5.29399075, 5.67126197],
       [5.61509076, 6.1309285 ],
       [6.18590347, 6.09410578],
       [7.16630941, 7.22719133],
       [4.05470826, 6.48127032],
       [5.79978164, 5.86930893],
       [4.82256361, 7.18593123]])

y_train[:200]

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

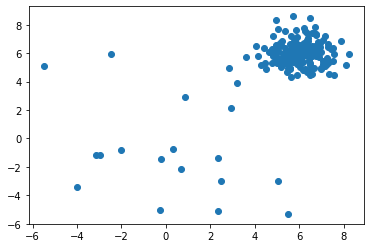
X_train の分布を可視化します :

import matplotlib.pyplot as plt
 
plt.scatter(X_train[:, 0], X_train[:, 1])

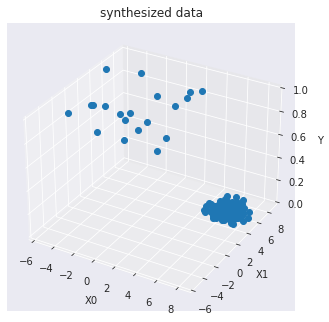
訓練データを可視化します :

import seaborn as sns
sns.set_style("dark")

from mpl_toolkits.mplot3d import Axes3D

X0 = X_train[:, 0]
X1 = X_train[:, 1]
Y = y_train

fig = plt.figure()
ax = Axes3D(fig)

ax.set_title("synthesized data")
 
ax.set_xlabel("X0")
ax.set_ylabel("X1")
ax.set_zlabel("Y")
 
ax.plot(X0, X1, Y, marker="o",linestyle='None')

 

モデル訓練

pyod.models.mcd.MCD 検出器をインポートして初期化し、そしてモデルを適合させます。

最小共分散行列式 (MCD) を使用したガウス分布データセット内の外れ値を検出します : 共分散の堅牢な推定器です。

最小共分散行列式・共分散推定器はガウス分布データ上で適用されますが、単峰性の対称な分布からドローされたデータ上でも関連性がある可能性があります。それは多峰なデータで使用されることを意味していません (MinCovDet オブジェクトを適合させるために使用されるアルゴリズムはそのような場合には失敗する傾向にあります)。多峰なデータセットを処理するためには射影追跡法を考慮するべきです。

最初に最小共分散行列式モデルを適合させてからデータの外れ値の degree として Mahalanobis 距離を計算します。

参照 :

  • Johanna Hardin and David M Rocke. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator. Computational Statistics & Data Analysis, 44(4):625–638, 2004.
  • Peter J Rousseeuw and Katrien Van Driessen. A fast algorithm for the minimum covariance determinant estimator. Technometrics, 41(3):212–223, 1999. 
from pyod.models.mcd import MCD

clf_name = 'MCD'
clf = MCD()
clf.fit(X_train)

MCD(assume_centered=False, contamination=0.1, random_state=None,
  store_precision=True, support_fraction=None)

訓練データの予測ラベルと外れ値スコアを取得します :

y_train_pred = clf.labels_  # binary labels (0: inliers, 1: outliers)
y_train_scores = clf.decision_scores_  # raw outlier scores

y_train_pred

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,
       1, 1])

y_train_scores[-40:]

array([4.24565000e+00, 4.22664796e-01, 2.20854837e+00, 3.19271455e+00,
       5.28318116e+00, 4.89035191e+00, 9.00245383e+00, 3.36891011e+00,
       6.41160123e+00, 3.70486129e+00, 8.97553458e-01, 3.23785753e+00,
       3.55922222e-01, 6.19169925e+00, 7.27336532e-01, 3.88522610e+00,
       1.08105367e+00, 1.42204980e+01, 6.55858782e-01, 1.46394676e+00,
       3.95907542e+00, 1.06528255e-01, 6.75944610e-01, 4.94017438e+00,
       5.62629894e+00, 8.14443303e+00, 1.92662344e+00, 7.81555289e+00,
       1.17055228e-01, 6.62232486e-01, 9.36051952e+01, 1.76344612e+02,
       1.03037866e+02, 2.51116697e+02, 1.79382377e+01, 2.37451925e+01,
       1.80881699e+02, 1.72118668e+02, 1.27494937e+02, 6.26970512e+01])

 

予測と評価

先に正解ラベルを確認しておきます :

y_test

array([0., array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

テストデータ上で予測を行ないます :

y_test_pred = clf.predict(X_test)  # outlier labels (0 or 1)
y_test_scores = clf.decision_function(X_test)  # outlier scores

y_test_pred

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])

y_test_scores[-40:]

array([ 5.9045124 , -2.01938422, -0.04809363,  1.579808  ,  7.29815783,
        2.75891915, 10.63424239,  1.69629951,  8.35181013,  3.87787154,
       -1.22952342,  2.30787057, -1.92598485,  8.78137251, -1.42671526,
        2.98254633, -1.05400309, 16.91238411, -1.38842923, -1.34779231,
        3.67815253, -1.95072358, -1.54857191,  3.38326885,  8.77706568,
       12.33489833, -0.87534863,  8.73047852, -1.9340466 , -1.4348534 ,
       26.06172492, 25.58479044, 25.93969245, 25.377791  , 22.11729834,
       23.73896701, 25.48826792, 26.29453172, 25.55043239, 25.38483225])

ROC と Precision @ Rank n pyod.utils.data.evaluate_print() を使用して予測を評価します。 

from pyod.utils.data import evaluate_print
# evaluate and print the results
print("\nOn Training Data:")
evaluate_print(clf_name, y_train, y_train_scores)
print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)

On Training Data:
MCD ROC:0.9986, precision @ rank n:0.95

On Test Data:
MCD ROC:1.0, precision @ rank n:1.0

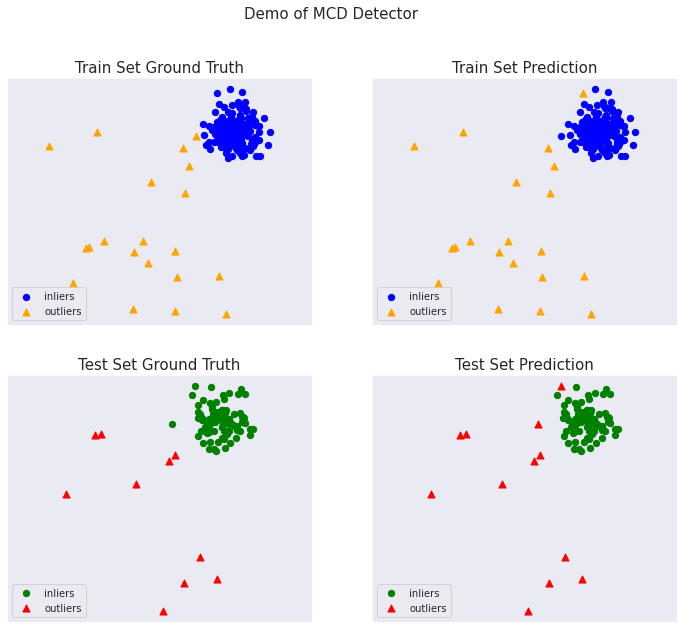
総ての examples に含まれる visualize 関数により可視化を生成します :

from pyod.utils.example import visualize
 
visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,
          y_test_pred, show_figure=True, save_figure=False)

 

以上



ClassCat® Chatbot

人工知能開発支援
◆ クラスキャットは 人工知能研究開発支援 サービスを提供しています :
  • テクニカルコンサルティングサービス
  • 実証実験 (プロトタイプ構築)
  • アプリケーションへの実装
  • 人工知能研修サービス
◆ お問合せ先 ◆
クラスキャット
セールス・インフォメーション
E-Mail：sales-info@classcat.com
クラスキャット