Prophet 1.0 : 診断 (Diagnostics) (翻訳/解説)
翻訳 : (株)クラスキャット セールスインフォメーション
作成日時 : 07/15/2021 (1.0)
* 本ページは、Prophet の以下のドキュメントを翻訳した上で適宜、補足説明したものです:
* サンプルコードの動作確認はしておりますが、必要な場合には適宜、追加改変しています。
* ご自由にリンクを張って頂いてかまいませんが、sales-info@classcat.com までご一報いただけると嬉しいです。

スケジュールは弊社 公式 Web サイト でご確認頂けます。
- お住まいの地域に関係なく Web ブラウザからご参加頂けます。事前登録 が必要ですのでご注意ください。
- ウェビナー運用には弊社製品「ClassCat® Webinar」を利用しています。
| 人工知能研究開発支援 | 人工知能研修サービス | テレワーク & オンライン授業を支援 |
| PoC(概念実証)を失敗させないための支援 (本支援はセミナーに参加しアンケートに回答した方を対象としています。) | ||
◆ お問合せ : 本件に関するお問い合わせ先は下記までお願いいたします。
| 株式会社クラスキャット セールス・マーケティング本部 セールス・インフォメーション |
| E-Mail:sales-info@classcat.com ; WebSite: https://www.classcat.com/ ; Facebook |
Prophet 1.0 : 診断 (Diagnostics)
交差検証
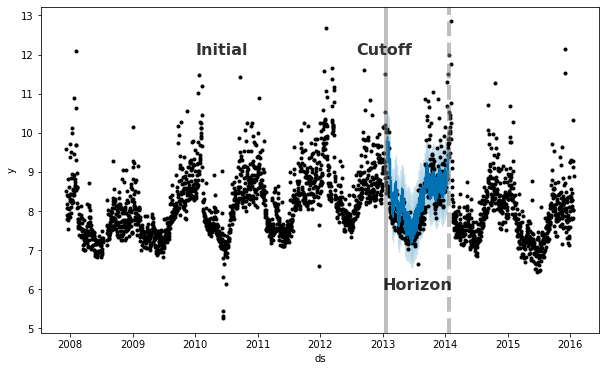
Prophet は履歴データを使用して予測誤差を測定するための時系列交差検証の機能を含みます。これは、履歴のカットオフポイントを選択し、それらの各々についてそのカットオフポイントまでのデータのみを使用してモデルを適合させることによって成されます。そして予測された値を実際の値と比較できます。この図は Peyton Manning データセット上のシミュレートされた履歴予測を示します、そこではモデルは 5 年の初期履歴に適合され、予測は 1 年の範囲で行なわれました。

Prophet 論文 はシミュレートされた履歴予測の更なる説明を与えます。
この交差検証手続きは cross_validation 関数を使用して履歴のカットオフの範囲のために自動的に成されます。予測範囲 (horizon)、それからオプションで初期訓練期間のサイズ (initial) とカットオフ日の間の間隔 (period) を指定します。デフォルトでは、initial 訓練期間は horizon の 3 倍に設定されて、カットオフは horizon の半分毎に行なわれます。
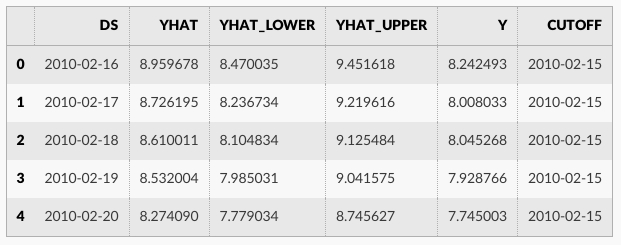
cross_validation の出力は各シミュレートされた予測日と各カットオフ日における真の値 y とサンプル外の予測値 yhat を持つデータフレームです。特に、予測はカットオフとカットオフ + horizon の間の総ての観測点のために行なわれます。そしてこのデータフレームは yhat vs. y の誤差測定値を計算するために使用されます。
ここでは 365 日の horizon の予測性能を評価するために交差検証を行ないます、最初のカットオフの 730 日の訓練データから始めて 180 日毎に予測を行ないます。この 8 年間の時系列では、これは合計 11 の予測に相当します。
from prophet.diagnostics import cross_validation
df_cv = cross_validation(m, initial='730 days', period='180 days', horizon = '365 days')
df_cv.head()
R では、引数 units は as.difftime により受け入れられるタイプでなければなりません、これは weeks か shorter です。Python では、initial, period と horizon のための文字列は Pandas Timedelta で使用される形式であるべきです、これは days or shorter の単位を受け取ります。
カスタム・カットオフは Python と R の cross_validation 関数の cutoffs キーワードへの日付のリストとして供給されることもできます。例えば、6 ヶ月間隔の 3 つのカットオフは次のような日付形式で cutoffs 引数に渡される必要があります :
cutoffs = pd.to_datetime(['2013-02-15', '2013-08-15', '2014-02-15'])
df_cv2 = cross_validation(m, cutoffs=cutoffs, horizon='365 days')
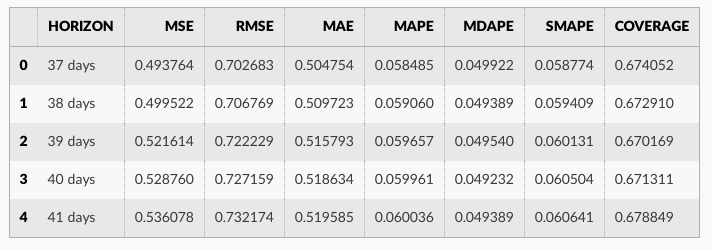
performance_metrics ユティリティはカットオフからの距離の関数として、予測性能の幾つかの有用な統計値を計算するために使用できます (yhat, yhat_lower と y に比較した yhat_upper )。計算される統計値は平均二乗誤差 (MSE)、二乗平均平方根誤差 (RMSE)、平均絶対誤差 (MAE)、平均絶対パーセント誤差 (MAPE)、中央値絶対パーセント誤差 (MDAPE)、そして yhat_lower と yhat_upper 範囲の推定値です。これらは horizon (ds minus カットオフ) によりソートされた後 df_cv の予測のローリング・ウィンドウ上で計算されます。デフォルトでは予測の 10% は各ウィンドウに含まれますが、これは rolling_window 引数で変更できます。
from prophet.diagnostics import performance_metrics
df_p = performance_metrics(df_cv)
df_p.head()
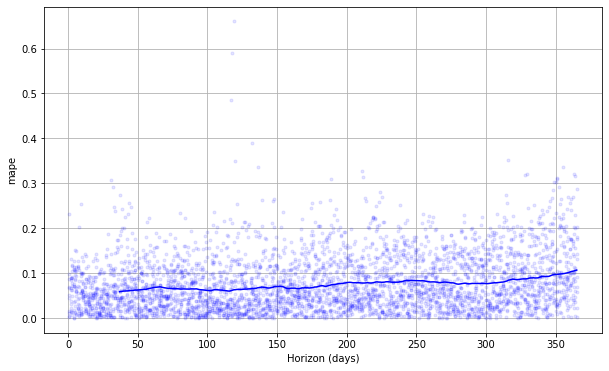
交差検証性能メトリクスは plot_cross_validation_metric で可視化できます、ここでは MAPE のために表示されます。ドットは df_cv の各予測のための絶対パーセント誤差を表します。青い線は MAPE を示し、そこでは平均はドットのローリング・ウィンドウに渡り取られます。この予測については、1ヶ月先への予測については 5% 前後の誤差が典型的で、1 年後の予測については誤差は 11% 前後にまで増加することがわかります。
from prophet.plot import plot_cross_validation_metric
fig = plot_cross_validation_metric(df_cv, metric='mape')
図のローリング・ウィンドウのサイズはオプション引数 rolling_window で変更できます、これは各ローリング・ウィンドウで使用する予測の比率を指定します。デフォルトは 0.1 で、各ウィンドウに含まれる df_cv からの行の 10% に相当し、これを増やすことは図での滑らかな平均カーブに繋がります。initial 期間は特に季節性と追加のリグレッサーでモデルの総ての成分を捕捉できるように十分に長くあるべきです : yearly 季節性のためには少なくとも 1 年、weekly 季節性のためには少なくとも 1 週間、等。
交差検証の並列化
交差検証は parallel キーワードの指定を設定することにより Python の並列モードで実行することもできます。4 つのモードがサポートされます :
- parallel=None (デフォルト, 並列化なし)
- parallel=”processes”
- parallel=”threads”
- parallel=”dask”
大きすぎない問題については、parallel=”processes” を使用することを勧めます。並列交差検証が単一マシン上で成されるときそれは最高の性能を達成します。大きな問題については、多くのマシン上で交差検証を行なうために Dask クラスタが使用されます。個別に Dask をインストール する必要があります、それは prophet と一緒にはインストールされないからです。
from dask.distributed import Client
client = Client() # connect to the cluster
df_cv = cross_validation(m, initial='730 days', period='180 days', horizon='365 days',
parallel="dask")
ハイパーパラメータ調整
changepoint_prior_scale と seasonality_prior_scale のような、モデルのハイパーパラメータを調整するために交差検証は利用できます。カットオフに渡る並列化、それら 2 つのパラメータの 4×4 グリッドによる、Python サンプルは下で与えられます。ここではパラメータは 30 日 horizon に渡り平均された RMSE で評価されますが、異なる性能メトリクスが異なる問題のために適切かもしれません。
# Python
import itertools
import numpy as np
import pandas as pd
param_grid = {
'changepoint_prior_scale': [0.001, 0.01, 0.1, 0.5],
'seasonality_prior_scale': [0.01, 0.1, 1.0, 10.0],
}
# Generate all combinations of parameters
all_params = [dict(zip(param_grid.keys(), v)) for v in itertools.product(*param_grid.values())]
rmses = [] # Store the RMSEs for each params here
# Use cross validation to evaluate all parameters
for params in all_params:
m = Prophet(**params).fit(df) # Fit model with given params
df_cv = cross_validation(m, cutoffs=cutoffs, horizon='30 days', parallel="processes")
df_p = performance_metrics(df_cv, rolling_window=1)
rmses.append(df_p['rmse'].values[0])
# Find the best parameters
tuning_results = pd.DataFrame(all_params)
tuning_results['rmse'] = rmses
print(tuning_results)
changepoint_prior_scale seasonality_prior_scale rmse
0 0.001 0.01 0.757694
1 0.001 0.10 0.743399
2 0.001 1.00 0.753387
3 0.001 10.00 0.762890
4 0.010 0.01 0.542315
5 0.010 0.10 0.535546
6 0.010 1.00 0.527008
7 0.010 10.00 0.541544
8 0.100 0.01 0.524835
9 0.100 0.10 0.516061
10 0.100 1.00 0.521406
11 0.100 10.00 0.518580
12 0.500 0.01 0.532140
13 0.500 0.10 0.524668
14 0.500 1.00 0.521130
15 0.500 10.00 0.522980
best_params = all_params[np.argmin(rmses)]
print(best_params)
{'changepoint_prior_scale': 0.1, 'seasonality_prior_scale': 0.1}
代わりに、上のループを並列化することによりパラメータの組合せについて並列化を行なうことができるでしょう。
Prophet モデルは調整を考えるかもしれない多くの入力パラメータを持ちます。ここに良い出発点であるかもしれないハイパーパラメータ調整のための幾つかの一般的な推奨があります。
調整可能なパラメータ
- changepoint_prior_scale : これは多分最も影響力のあるパラメータです。トレンドの柔軟性、特にトレンド変化点でどのくらいのトレンド変化があるかを決定します。このドキュメントで説明されているように、それが小さすぎれば、トレンドは過小適合になりそしてトレンド変化でモデル化されるべき分散は代わりにノイズ項で処理されることになります。それが大きすぎれば、トレンドは過剰適合となり最も極端な場合には yearly 季節性を捕捉するトレンドで終わる可能性があります。0.05 のデフォルトは多くの時系列のために動作しますが、これは調整できます ; [0.001, 0.5] の範囲がおそらく概ね適切です。このようなパラメータ (正則化ペナルティ ; これは実質的には lasso ペナルティです) はしばしば対数スケールで調整されます。
- seasonality_prior_scale : このパラメータは季節性の柔軟性を制御します。同様に、大きな値は季節性を大きな変動に適合させることを可能にし、小さい値は季節性の大きさを縮小します。デフォルトは 10. で、これは基本的には正則化を適用しません。これはここでは滅多に過剰適合を見ないからです (それは truncated フーリエ級数でモデル化されているという事実により固有の正則化はありますので、それは本質的には low-pass フィルタ処理されています)。それを調整するための合理的な範囲は多分 [0.01, 10] です ; 0.01 に設定するとき季節性の大きさが非常に小さくなるように強制されることを見出すはずです。これはまた対数スケール上でも意味がある傾向にあります、何故ならばそれはリッジ回帰のように実質的には L2 ペナルティであるからです。
- holidays_prior_scale : これは休日効果に適合させるための柔軟性を制御します。seasonality_prior_scale と同様に、それは 10.0 がデフォルトです、これは基本的には正則化を適用しません、何故ならば通常は休日の複数の観測を持ち上手く効果の推定を行えるからです。これは seasonality_prior_scale と同様に [0.01, 10] の範囲でも調整できます。
- seasonality_mode : オプションは [‘additive’, ‘multiplicative’] です。デフォルトは ‘additive’ ですが、多くのビジネス時系列は乗法的季節性を持ちます。これは時系列を単に見て、季節的変動の大きさが時系列の大きさとともに増大するかを見ることにより最善に識別されます (乗法的季節性についてはここのドキュメントを見てください) が、それが可能ではないとき、それは調整できるでしょう。
多分調整 (可能)?
- changepoint_range : これはトレンドが変化することが許容されている履歴の割合です。これは履歴の 0.8, 80% がデフォルトで、時系列の最後の 20% ではどのようなトレンド変化にもモデルが適合されないことを意味します。これはかなり保守的で、(上手く適合するために十分な走路が残されていない) 時系列の本当に最後でトレンド変化への過剰適合を回避するためです。ループで人間によれば、これは非常に容易に視覚的に識別できます : 最後の 20% で予測が上手くいかないかを非常に明瞭に見ることができます。完全自動設定では、保守性を低くすることは有益かもしれません。上で説明されたようにカットオフによる交差検証でこのパラメータを効果的に調整することは可能ではないかもしれません。時系列の最後の 10% のトレンド変化から一般化するモデルの能力は、最後の 10% でトレンド変化を持たないかもしれない先のカットオフを見ることから学習することは困難です。従って、このパラメータは多分調整されないことが良いです、大規模な数の時系列に渡る場合を多分除いて。その設定では、[0.8, 0.95] が妥当な範囲であるかもしれません。
調整されない傾向にあるパラメータ
- growth : オプションは ‘linear’ と ‘logistic’ です。これはおそらく調整されません ; 既知の飽和点とそのポイントに向けての成長がある場合、それは含まれて logistic トレンドが使用され、そうでなければそれは linear です。
- changepoints : これは変化点の位置を手動で指定するためのものです。デフォルトは None で、これはそれらを自動的に配置します。
- n_changepoints : これは自動的に配置された変化点の数です。25 のデフォルトは典型的な時系列でトレンド変化を捕捉するために十分であるはずです (少なくとも Prophet が上手く動作するタイプ)。変化点の数を増やしたり減らしたりするよりも、それらのトレンド変化で柔軟性を増やしたり減らしたりすることに焦点を当てることがより効果的かもしれません、これは changepoint_prior_scale で成されます。
- yearly_seasonality : デフォルト (‘auto’) では、これは年間データがあれば yearly 季節性をオンに、そうでなければオフにします。オプションは [‘auto’, True, False] です。1 年間以上のデータがあれば、HPO の間にこれをオフにしようとするよりも、それをオンのままにして、seasonality_prior_scale を調整して季節的効果を無効にすることがより効果的であるかもしれません。
- weekly_seasonality : yearly_seasonality と同じです。
- daily_seasonality : yearly_seasonality と同じです。
- holidays : これは指定された休日のデータフレームを渡すためです。休日効果は holidays_prior_scale で調整されます。
- mcmc_samples : MCMC が使用されるか否かは時系列の長さとパラメータ不確実性の重要度のような要因で決定される可能性があります (これらの考慮点はドキュメントで説明されます)。
- interval_width : Prophet は予測 yhat に対する yhat_lower と yhat_upper のように、各成分に対して不確定区間を返します。これらは事後予測分布の分位点として計算され、interval_width はどの分位点を使用するかを指定します。0.8 のデフォルトは 80% 予測区間を提供します。95% 区間を望む場合はそれを 0.95 に変更できます。これは不確定区間だけに影響し、そして予測 yhat は全く変更しませんので、調整される必要はありません。
- uncertainty_samples : 不確定区間は事後予測区間の分位点として計算され、事後予測区間は Monte Carlo サンプリングで推定されます。このパラメータは使用するサンプリングの数です (デフォルトは 1000)。予測のための実行時間はこの数で線形です。それを小さくすると不確定区間の分散 (Monte Carlo 誤差) を増加させ、大きくすればその分散を減じます。従って、不確実性推定がギザギザ (jagged) に見えるなら、それらを更に滑らかにするためにこれを増加できますが、変更される必要はないかもしれません。interval_width と同様に、このパラメータは不確定区間に影響を与えるだけで、それの変更は予測 yhat にはどのようにも影響しません ; それは調整される必要はありません。
- stan_backend : pystan と cmdstanpy の両者がセットアップされる場合、バックエンドが指定できます。予測は同じで、これは調整されません。
以上
